James Park examines whether the third set is critical to recurve competition.
Is the third set in a match more important than the other sets? Archers lose score for many reasons. For example, they can lose points due to not aiming perfectly, moving as they operate the clicker or release device, wind drift, or bow cant variation.
When there are several independent score-loss mechanisms happening at once we can expect the Central Limit Theorem to apply. That means that we can expect the distance by which they miss the centre of the target to be normally distributed. As the ability of the archer increases that distribution should still be normal, but the standard deviation will start to decrease.
We should be able to model an archer’s score by overlaying a normal distribution – with the standard deviation selected to match the archer’s ability – on the target face and seeing what proportion of the archer’s arrows hit each target ring.
For the mathematically inclined readers, I do this using a standard deviation defined by:
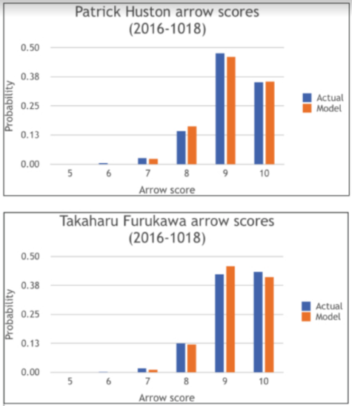
We can then examine the arrow score distribution for an archer and see if it matches this model. For example, here they are for Patrick Huston and Takaharu Furukawa.
I have used each of the ranking rounds they shot in major international events from 2016–2018. The match between the actual results and the model is quite impressive.
You can see that they mostly shoot 9s and 10s but have the occasional 7 or 8, as expected. We can then model their expected scores for three arrow sets and compare those to the actual results.
This is only viable for the top group of archers as archers lower down don’t shoot enough sets in major international competition to give statistically viable results; the less capable archers lose in the early rounds and hence don’t get to shoot enough matches.
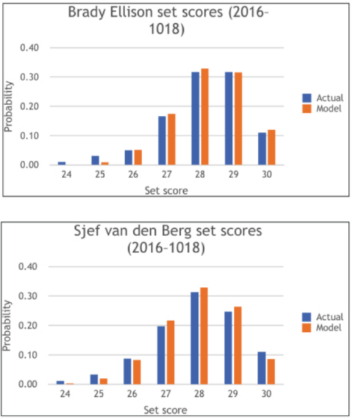
Here are the results for Brady Ellison and Sjef van den Berg. Again, the match between the actual results and the model is excellent.
We can then examine the average set score for each archer and the average for the third set, to see if the third set is especially important. I have considered scores for Kim Woojin, Crispin Duenas, Patrick Huston, Brady Ellison, Mauro Nespoli, Taylor Worth, Ryan Tyack, Sjef van den Berg, Takaharu Furukawa, Steve Wijler, Lee Woo Seok, Wei
Chun Heng, Atanu Das and Thomas Chirault; fourteen of the World’s most capable male recurve archers.
We also need to test to determine if any differences are statistically significant or not. For this, I have used a ‘T test’. For twelve of the archers the average score for their third set was not significantly different to the average for all their sets. For two of the fourteen (Nespoli and Worth) there was a significant difference – they would be dangerous competitors in that third set.
 These results suggested that the third set was not ‘special’ or ‘different’ but was handled by the top archers just the same as their other sets in a match. I have then examined the results from major competitions during 2016-2018 to see if, for those archers, winning or losing the third set was correlated to them then winning or losing the match.
These results suggested that the third set was not ‘special’ or ‘different’ but was handled by the top archers just the same as their other sets in a match. I have then examined the results from major competitions during 2016-2018 to see if, for those archers, winning or losing the third set was correlated to them then winning or losing the match.
Let us first look at Kim Woojin, a wonderfully capable and very successful archer. His average set score over 47 matches was 28.39 and higher than all other archers I considered other than Lee Woo Seok at 28.60. Hence, we could imagine that Kim should win most matches (which he does).
Of those 47 matches, he won 38. However, in those 47 matches, he won the third set but lost the match on four occasions and lost the third set but won the match on 2 occasions.
Brady Ellison had 45 matches in that period, winning 34. In those matches, he won the third set but lost the match on four occasions and lost the third set but won the match on six occasions.
Steve Wijler won 22 of 29 matches. He lost the third set but won the match on five occasions and won the third set and lost the match once. The other top archers showed very similar results.
From these results and noting the average scores for the third set, it seems quite compelling that, at least for the top archers, the archers treat the third set no differently to the other sets in a match. It might be different for less capable archers who are not used to the pressures of match play, but there is insufficient data to test that.
In a future article, I will show how we can use the modelling of the archers’ scores to calculate the probabilities of them winning a match or a whole event.