Keeping a low profile

I am an engineer – my career has been in telecommunications, but my recent PhD studies were in mechanical engineering. For my PhD I was primarily interested in arrow behaviour, both during the power stroke of the bow and then while in free flight on its way to the target, which necessarily involves consideration of airflow and of beams flexing.

Consequently, I was quite interested to see Fuse start to market ‘Blade’ stabilisers with elliptical cross-sections. They interested me from two points of view – how did that affect their performance in wind, and could Fuse make it stiff enough? You also have the interesting challenge of how to fix it to the bow so that it is oriented correctly every time.

While the archer is aiming, gusts of wind push on both the archer and his or her equipment. Wind gusts pushing on the stabiliser act to rotate the bow about its centre of mass (it is a little more complicated than that because the archer is also holding it, so the forces on the stabiliser act to rotate the bow in the archer’s hand). This disturbs the archer’s aim and results in score loss. From an engineer’s point of view, we have a moment from the force from the wind on the stabiliser and a lever arm about half the length of the stabiliser. If the force from the wind on the stabiliser is greater, the archer’s aim is affected to a greater extent.

The force from the air pushing on an object is given by the equation:

where p is the air density, V is the wind velocity, A is the area and C_d is the drag coefficient. We can consider the air density to be constant, and that different stabilisers are subject to the same air velocity. Consequently, any differences in the forces on them from gusts of wind will come from differences in their areas and drag coefficients.

The area is simply that area seen from the wind direction. For a side wind it is the length of the stabiliser multiplied by the height of the stabiliser. Consequently, for a round stabiliser rod, it is the length multiplied by the diameter. For an elliptical stabiliser rod it is the length multiplied by the minor axis. It is considerably more complex for a multi-rod stabiliser as the air flow over one rod can strongly influence the air flow over others.

The drag coefficient is more challenging, but can be readily found for standard cross-sections from tables in engineering handbooks or on the internet. For a round cross-section it is typically about 1.1. For an elliptical cross-section the drag coefficient depends upon the ratio of the major-to-minor axis. It is lower than that for a round rod of the same minor axis because the elliptical shape helps the air get back together again after passing the rod better than for a round rod, which reduces the area of lowered pressure downwind from the rod. My blade stabiliser has a major axis of 25.4mm and a minor axis of 10.7mm, giving a ratio of 2.4. That suggests a drag coefficient of about 0.5, which is considerably less than that of a round rod.

I have several stabiliser set-ups with round rods. The diameter of one is 22.3mm and the other has a diameter of 16.3mm. Consequently, assuming that the elliptical stabiliser is edge-on to the side wind, its drag force is approximately 22 per cent of that for the larger diameter round stabiliser and approximately 30 per cent of that for the smaller diameter round stabiliser, which are considerable reductions and should be quite noticeable to the archer in a gusty wind.

For example, in a side wind of three m/s, the force on the elliptical stabiliser will be 0.029N. For the larger diameter round stabiliser it will be 0.133N, and for the smaller diameter stabiliser it will be 0.097N. (Where 1N is the force needed to accelerate a mass of 1kg at 1 m/s².)

It is also necessary to consider lift forces on the stabiliser due to a side wind. That is, a side wind can generate a force on the stabiliser in the vertical plane. The lift can be treated in the same manner as for the drag, using the relevant lift coefficient instead of the drag coefficient. For the round rods the lift coefficient is zero and hence the lift is also zero, which is useful. For the elliptical cross-section the lift coefficient depends upon the angle of the stabiliser in relation to the wind: it is typically 2pi times the angle of attack, where the angle is in radians. For a side wind of three metres per second and an angle of two degrees (which is readily achievable) the lift will be approximately 0.010N.

The total force from the side wind on the stabiliser is therefore the vector sum of the lateral and vertical forces, and so for the elliptical cross-section it will be 0.031N, which is still considerably less than that for the round cross-sections (23 per cent and 31 per cent).

Different stabiliser profiles will perform differently in the wind

Consequently, it seems that allowing for both drag and lift still has the elliptical profile giving a considerable reduction in the force on the stabiliser from wind, which is a nice advantage.

I asked my shooting partner, David Giulieri, to try a direct comparison on a windy day, by swapping between similarly configured stabilisers on the one bow, and he certainly noticed the force reduction between the two types of stabiliser cross section.

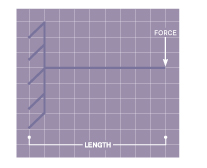
The next thing to consider is if an elliptical cross-section be made sufficiently stiff. A cantilevered beam is shown below. It is similar to a stabiliser:

The deflection at the end of the beam is given by:

where W is the deflection, F is the force applied at the end of the beam, L is the length of the beam, E is Young’s Modulus and I is the second moment of area (which is determined by the cross-sectional shape of the beam). Note that the deflection depends upon the length cubed.

The second moment of area is a measure of how far the material in the beam is on average from the beam’s neutral axis. For a given beam cross-sectional area it is more difficult to flex a thick beam than a thin beam. That is, the second moment of area depends strongly upon the beam’s height and cross-section. For example, a large diameter stabiliser is much more difficult to flex than a small diameter stabiliser of the same area and length

Gusty wind can affect an archer’s aim, so low-profile stabilisers aim to minimise this effect

Consequently, because the blade stabiliser is quite wide, we can expect it to be very stiff laterally. Its minor axis is, however, smaller than that of my other two stabilisers so as a simple elliptical tube we would expect its stiffness to be lower in the vertical plane. However, it is not a simple elliptical tube but incorporates a vertical beam down its centre, which adds substantially to its stiffness. The Blade ES has the same cross sectional shape as the Blade but is larger, so its stiffness can be expected to be considerable increased over that of the original Blade.

Overall, the engineering impresses me, the mathematics tells me they should work well, and that matches my practical experience in testing them.